Die Lambert'sche W-Funktion

Es wird folgende Funktion betrachtet:

.

1. Nullstellen

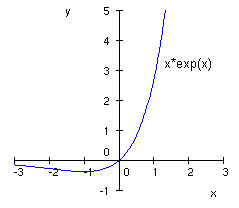
Da ist, ist x = 0 die einzige Nullstelle von f.

2. Ableitungen

3. Lokale Extrema

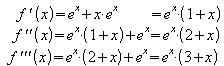
notwendige Bedingung:

Dies ist nur für x = –1 erfüllt.

hinreichende Bedingung:

x = –1 ist also lokale Minimalstelle.

lokales Minimum:

4. Wendepunkte

notwendige Bedingung:

Dies ist nur für x = –2 erfüllt.

hinreichende Bedingung:

x = –2 ist also Wendestelle mit Steigungsminimum (RL-Wendestelle).

RL-Wendepunkt:

5. Monotoniebereiche

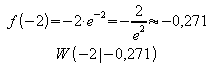
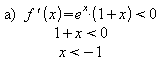
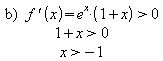
Für x < –1 ist f also streng monoton fallend und für x > –1 ist f streng monoton wachsend.

6. Umkehrfunktionen

Wird f jeweils auf einen Monotoniebereich eingeschränkt, so ergeben sich umkehrbare Funktionen.

a)

Die Umkehrfunktion von f₁

ist der obere reelle Zweig der Lambert'schen W-Funktion:

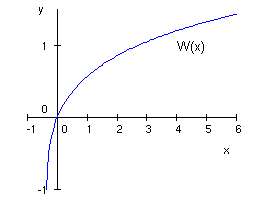
b)

Die Umkehrfunktion von f₂

ist der untere reelle Zweig der Lambert'schen W-Funktion:

7. Ableitungen der Lambert'schen W-Funktion

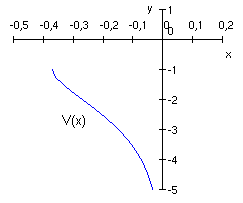
Mit der Regel zum Ableiten der Umkehrfunktion

ergibt sich:

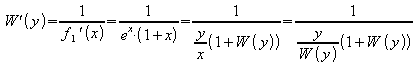
Nach Umbenennen der Variablen:

Entsprechend folgt:

8. Weitere Beziehungen

Aus

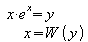
ergibt sich

.

Nach Umbenennen der Variablen:

.

Logarithmieren führt auf

.

Umgestellt:

.

9. Die W-Funktion auf dem Computer

Auf Taschenrechnern steht die W-Funktion nicht zur Verfügung. Um Berechnungen mit der W-Funktion auszuführen, wird daher ein Computeralgebrasysteme wie z.B. Maple, Derive, MathCad, MuPAD usw.benötigt.

In MuPAD werden zwei Funktionen angeboten:

lambertW(x): der obere reelle Zweig,

lambertV(x): der untere reelle Zweig.

Beispiel:

float(lambertW(1))

          0.5671432904

float(lambertW(exp(1)))

          1.0

float(lambertW(4))

          1.202167873

float(lambertV(-0.1))

          -3.577152064

float(lambertV(-0.3))

          -1.781337023

float(lambertV(-0.35))

          -1.349717252

float(lambertV(-1))

          lambertV(-1.0)

Home