(1) ![]()
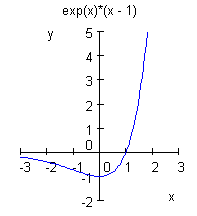
a) y > 0:
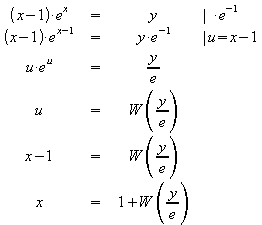
Beispiel: ![]()
Berechnung mit MuPAD:
float(1 + lambertW(2/exp(1)))
1.463055513
b) –1 < y < 0:
Die Gleichung
![]()
hat zwei Lösungen:
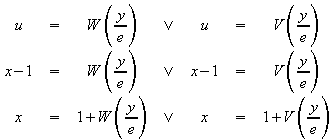
Beispiel: ![]()
float(1 + lambertW(-1/(2*exp(1))))
0.768039047
float(1 + lambertV(-1/(2*exp(1))))
-1.67834699
(2) ![]()
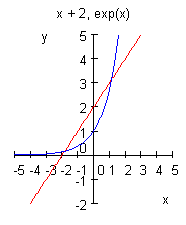
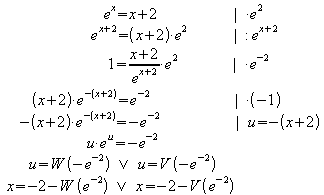
float(-2 - lambertW(-exp(-2)))
-1.84140566
float(-2 - lambertV(-exp(-2)))
1.146193221
(3) ![]()
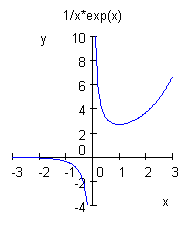
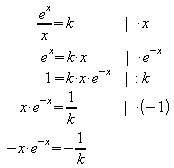
a) k < 0:
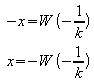
Beispiel: k = –2
float(-lambertW(-1/-2))
-0.3517337112
b) k > 0:
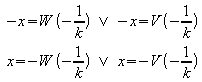
Beispiel: k = 4
float(-lambertW(-1/4))
0.3574029562
float(-lambertV(-1/4))
2.153292364
(4) ![]()
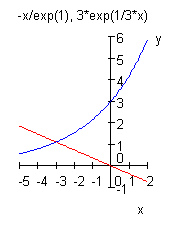
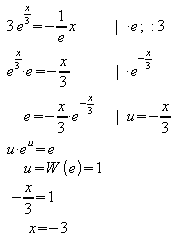
(5) ![]()
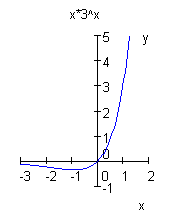
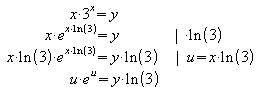
a) y > 0:
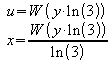
Beispiel: y = 4
float(lambertW(4*ln(3))/ln(3))
1.141441887
b) y < 0:
![]()
Beispiel: y = –0,2
float(lambertW(-0.2*ln(3))/ln(3))
-0.2686691116
float(lambertV(-0.2*ln(3))/ln(3))
-2.170276592
(6) ![]()
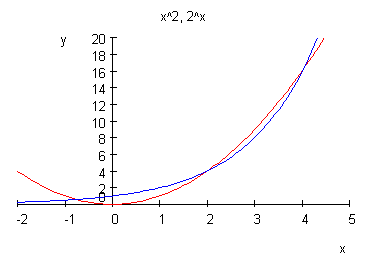
a) x > 0:
Die beiden Lösungen x = 2 und x = 4 sind natürlich sofort zu sehen. Zur Übung sollen diese Lösungen aber auch noch durch Auflösen der Gleichung unter Verwendung der W-Funktion ermittelt werden.
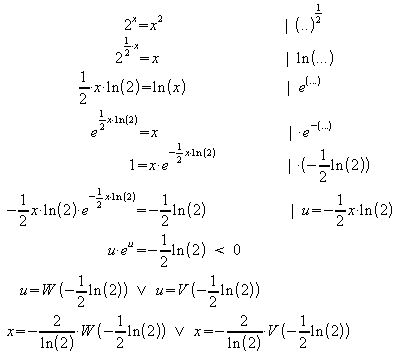
float(-2/ln(2)*lambertW(-1/2*ln(2)))
2.0
float(-2/ln(2)*lambertV(-1/2*ln(2)))
4.0
b) x < 0:
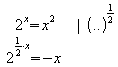
Mit den gleichen Umformungen wie in a) ergibt sich:
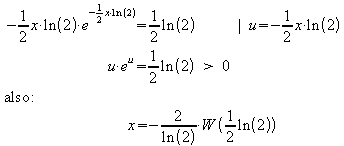
float(-2/ln(2)*lambertW(1/2*ln(2)))
-0.766664696
(7) ![]()
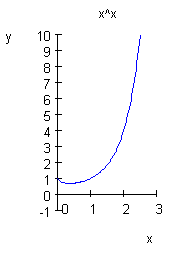
Berechnung des Tiefpunktes mit MuPAD:
f := x -> x^x :
f'(x)
x x - 1
x ln(x) + x x
numeric::solve(f'(x) = 0,x)
{0.3678794411}
f(0.3678794411)
0.6922006276
Für y < 0,6922... gibt es keine Lösungen.
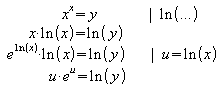
a) 0,6922 < y < 1:
In diesem Fall ist ln(y) < 0, also gibt es zwei Lösungen:
![]()
Beispiel: y = 0,9
float(exp(lambertW(ln(0.9))))
0.8881353288
float(exp(lambertV(ln(0.9))))
0.03006536849
b) y > 1:
In diesem Fall ist
![]() .
.
Beispiel: y = 5
float(exp(lambertW(ln(5))))
2.129372483
(8) ![]()
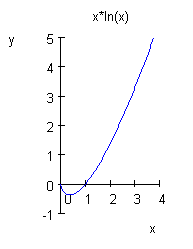
Das Minimum wird an der Stelle ![]() angenommen
und beträgt
angenommen
und beträgt ![]() .
.
Für ![]() gibt es zwei
Lösungen, für y > 0 eine Lösung.
gibt es zwei
Lösungen, für y > 0 eine Lösung.
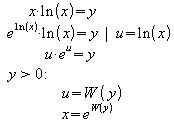
Beispiel: y = 2
float(exp(lambertW(2)))
2.345750755
(9) ![]()
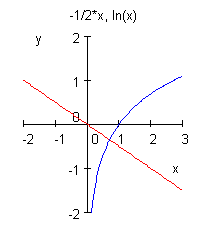
... bleibt dem Leser als leichte Übung überlassen ;-)